双数组前缀树

一、前缀树

前缀树，又称字典树。常见的场景为大规模词库下做词匹配、词前缀匹配、词频统计等。目前唯一碰到的业务场景只有自建 UGC 风控的违禁词检测。

经典前缀树基于多叉树结构实现，组成字符串的字符全集数量决定了多叉树的阶。如下图为字符串集合 ab, abc, bc, d, da, dda 形成的前缀树。

前缀树的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销，相较于哈希等能够显著降低失配字符串的匹配耗时。

二、前缀树的缺陷

虽然空间换时间是使用前缀树的共识，但空间也是有代价的。构建英文词典的前缀树，需要维护一个 26 叉树。即在每个词都没有公共前缀的前提下，平均长度为 Length 的 N 个词，使用的空间将至少达到 $26 * N * Length$ 个 int (节点指针的大小)

英语用 26 个符号编码就能构建所有的词，但用于中日韩表意文字 (CJK Unified Ideographs)，26 个符号编码远远不够。GB-2312 收录有 6763 个汉字，GB-18030 更是收录了 70244 个汉字。如果需要基于一本中文词典构建前缀树，由于符号数量的扩展，常量 26 将突增为几百、几千甚至几万。这就无谓地浪费了空间。

在英文世界应用良好的经典前缀树结构出现了水土不服。为了解决这个问题，就出现了压缩状态空间的双数组前缀树 (Double-Array Trie)

三、双数组前缀树

前缀树的本质是一个确定有限状态自动机 (DFA, Deterministic Finite Automaton) ，确定当前状态和转移函数，能够确定性地转移到下一个状态。

图 1 的内容用确定有限状态机表示为

• 有限的状态集合$Q = start, a1, b1, d1, b2, c2, a2, d2, c3, a3$ (见图示 浅灰色字)
• 输入字母表 $\sum = {a, b, c, d}$
• 开始状态 $s = start$
• 终止状态集 $F = b2, c2, a2, c3, a3$
• 状态转移表描述为：

|       | a       | b       | c       | d    |
| ----- | ------- | ------- | ------- | ---- |
| start | a1      | b1      |         | d1   |
| a1    |         | b2(end) |         |      |
| b1    |         |         | c2(end) |      |
| d1    | a2(end) |         |         | d2   |
| b2    |         |         | c3(end) |      |
| d2    | a3(end) |         |         |      |

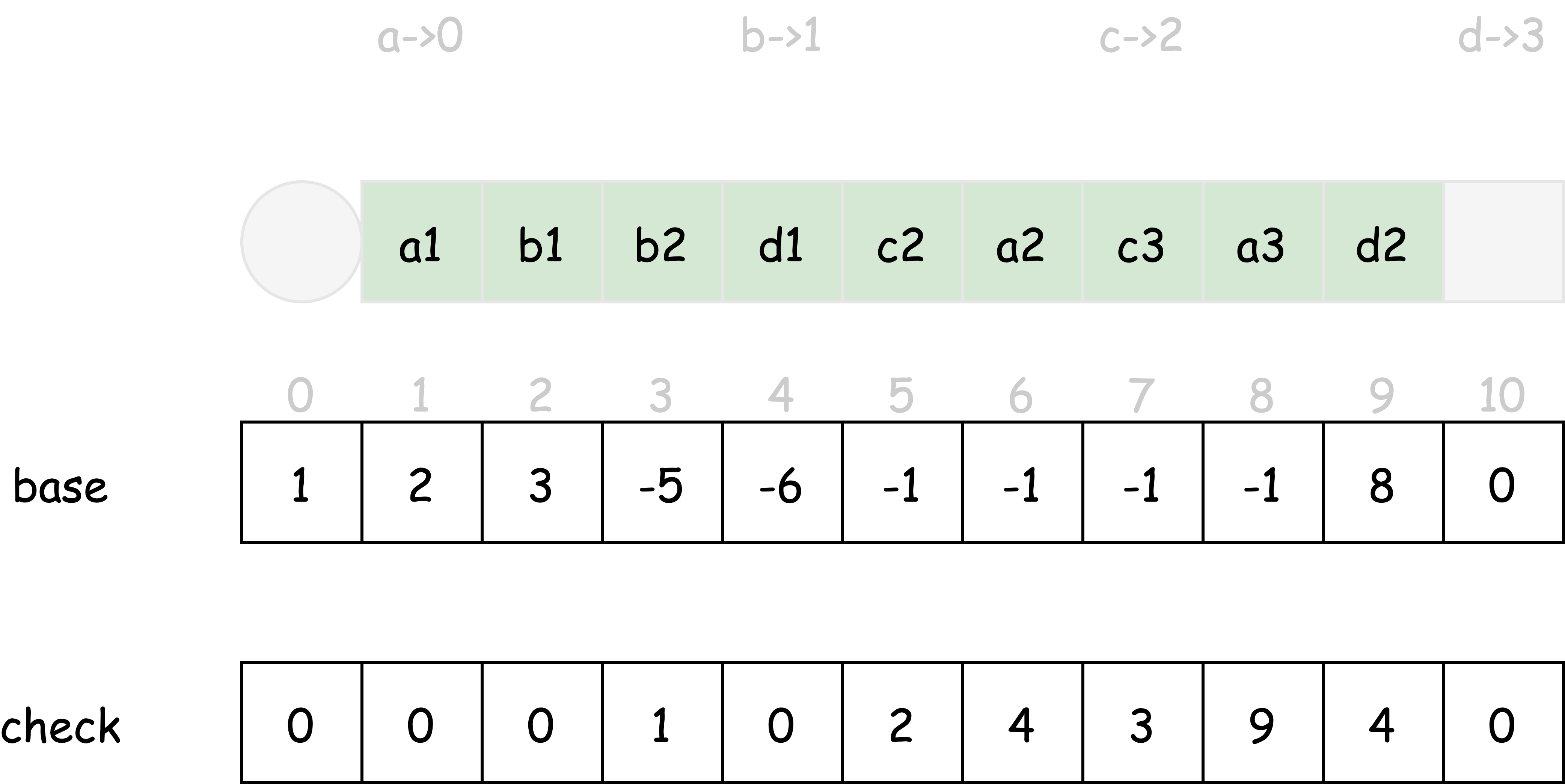
从状态机的角度看，状态集不大，仅包含 10 种状态，其中 4 种 (a2, a3, c2, c3) 可以统一归结为终态。即为了这一个包含 7 种状态的状态机，构建了 50 多节点的多叉树来完整状态转移函数。双数组前缀树利用双数组，以实现缩小构建状态转移函数的节点数量。

四、使用双数组前缀树

词匹配可以看做是构成词的若干字符(输入)，使状态机多次进行状态转移，最终是否能到达终态的一个验证流程。为了方便状态转移函数的构建，构成词的若干字符(输入) 有必要映射成整数，便于进行运算。有下列两个公式：

• index(a) -> b 。图2中, index(‘a’) -> 0, index(‘b’) -> 1, index(‘c’) -> 2, index(’d’) -> 3
• stateY = base[stateX] + index(‘a’)

词 abc 的验证流程如下(请暂且忽略 check 数组，稍后解释)

1. 起始状态为 start ，即用数组下标记做 0
2. 输入字符 a ，$stateY = base[0] + index(a) = 1 + 0 = 1$，现在状态数组下标 1，即 a1
3. 输入字符 b ，$stateY = base[1] + index(b) = 2 + 1 = 3$，现在状态数组下标 3，即 b2
4. 输入字符 c ，$stateY = base[3] + index(c) = 5 + 2 = 7$，现在状态数组下标 7，即 c3

从状态转移来看，整个流程与经典前缀树一致，start -> a1 -> b2 -> c3 。仅仅一个 base 数组就构建了一个状态转移函数。但是，有个致命的问题？

再举个例子，词 abb 不属于词典

1. 起始状态为 start ，即用数组下标记做 0
2. 输入字符 a ，$stateY = base[0] + index(a) = 1 + 0 = 1$，现在状态数组下标 1，即 a1
3. 输入字符 b ，$stateY = base[1] + index(b) = 2 + 1 = 3$，现在状态数组下标 3，即 b2
4. 输入字符 b ，$stateY = base[3] + index(b) = 5 + 1 = 6$，现在状态数组下标 6，即 a2

状态 b2 -> a2 不可转移，但状态转移函数没有发现这个问题。base 数组构建了状态转移函数，check 数组恰恰是用来确认状态转移是否成立的。试想，前缀树中每个状态的前置状态都是确定且唯一的。check 数组就存储当前状态的前置状态。第三个公式：

• stateX = check[stateY]

回头看看词 abb 验证流程的第 4 步，由于 check[6] != 3 ，所以状态转移 b2 -> a2 不成立。

至于如何描述终止状态，可以用 base 数组的正负符号描述是否为终态。其中负号为终止状态。当然，用 check 数组的正负号也行，或者其他方式。

五、构建双数组前缀树

双数组前缀树的查询，与经典前缀树的查询同样高效。但构建一个双数组前缀树，代价却非常巨大。

以上例中的词典 ab, abc, bc, d, da, dda 举例：

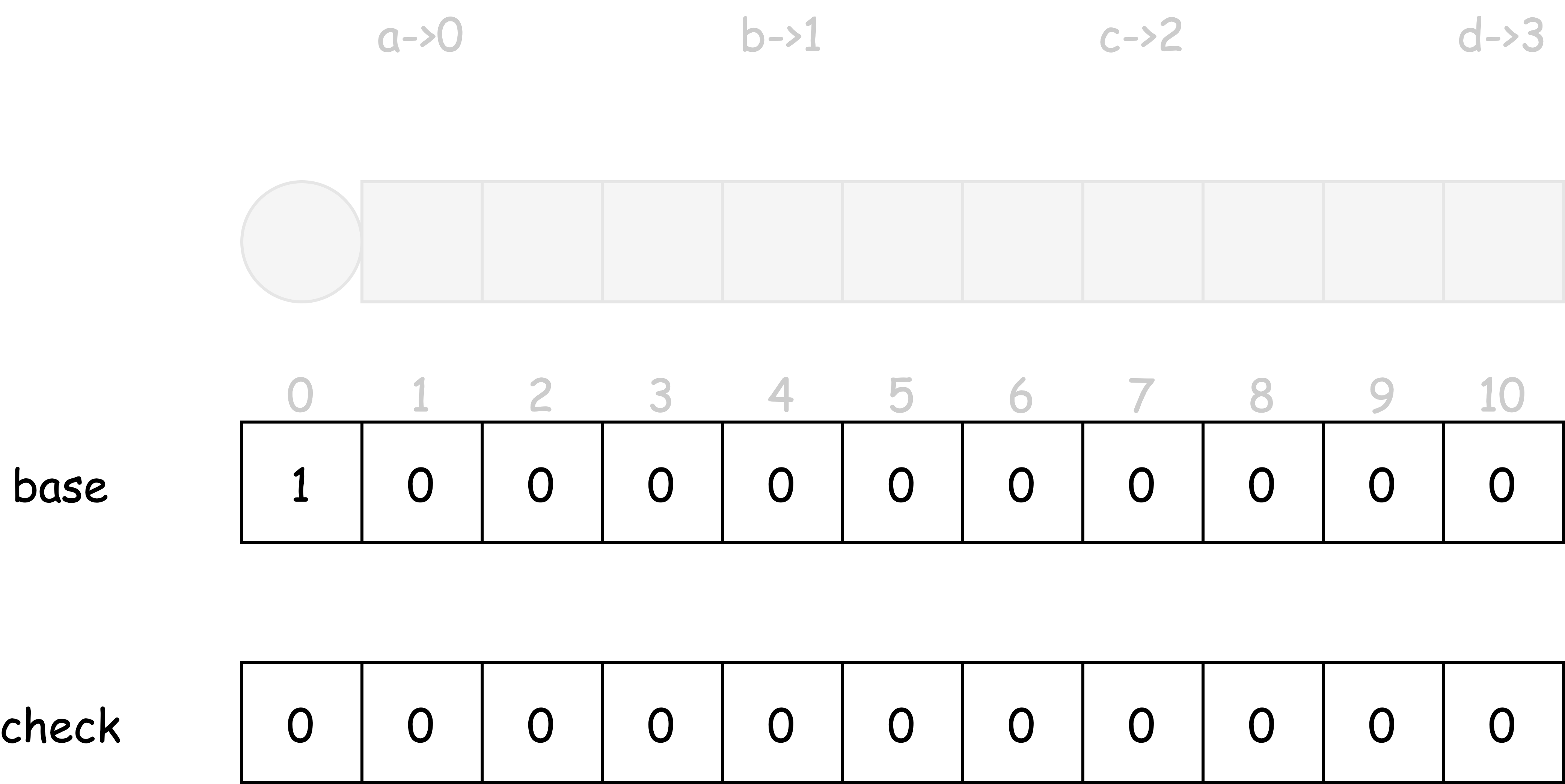
首先确定输入字符集 $\sum = {a, b, c, d}$ 的映射，index(‘a’) -> 0, index(‘b’) -> 1, index(‘c’) -> 2, index(’d’) -> 3。

并初始化 base, check 两个数组，初始值全为 0。（如果后续发现数组长度不够，自行通过相关算法扩展数组）

初始状态 start 可以分别基于输入字符 a, b, d，转移到状态 a1, b1, d1 。故有下列几个公式

• $a1 = base[start] + index(a) = base[start] + 0$
• $b1 = base[start] + index(b) = base[start] + 1$
• $d1 = base[start] + index(d) = base[start] + 3$

$base[start] = 1$ 时，$base[1]$, $base[2]$, $base[4]$ 都为 0 （表示未被使用）

将 $base[1]$, $base[2]$, $base[4]$ 改写为 1 （表示已被使用），同时记 $check[1]$, $check[2]$, $check[4]$ 为前置状态 $start=0$

状态 a1 可以基于输入字符 b 转移到状态 b2，有

• $b2 = base[a1] + index(b) = base[a1] + 1$

由于下标为 2 的数组元素已经被占用，选择 $base[a1] = 2$ 则 $b2 = 3$，分别将 $base[3]$, $check[3]$ 改写。

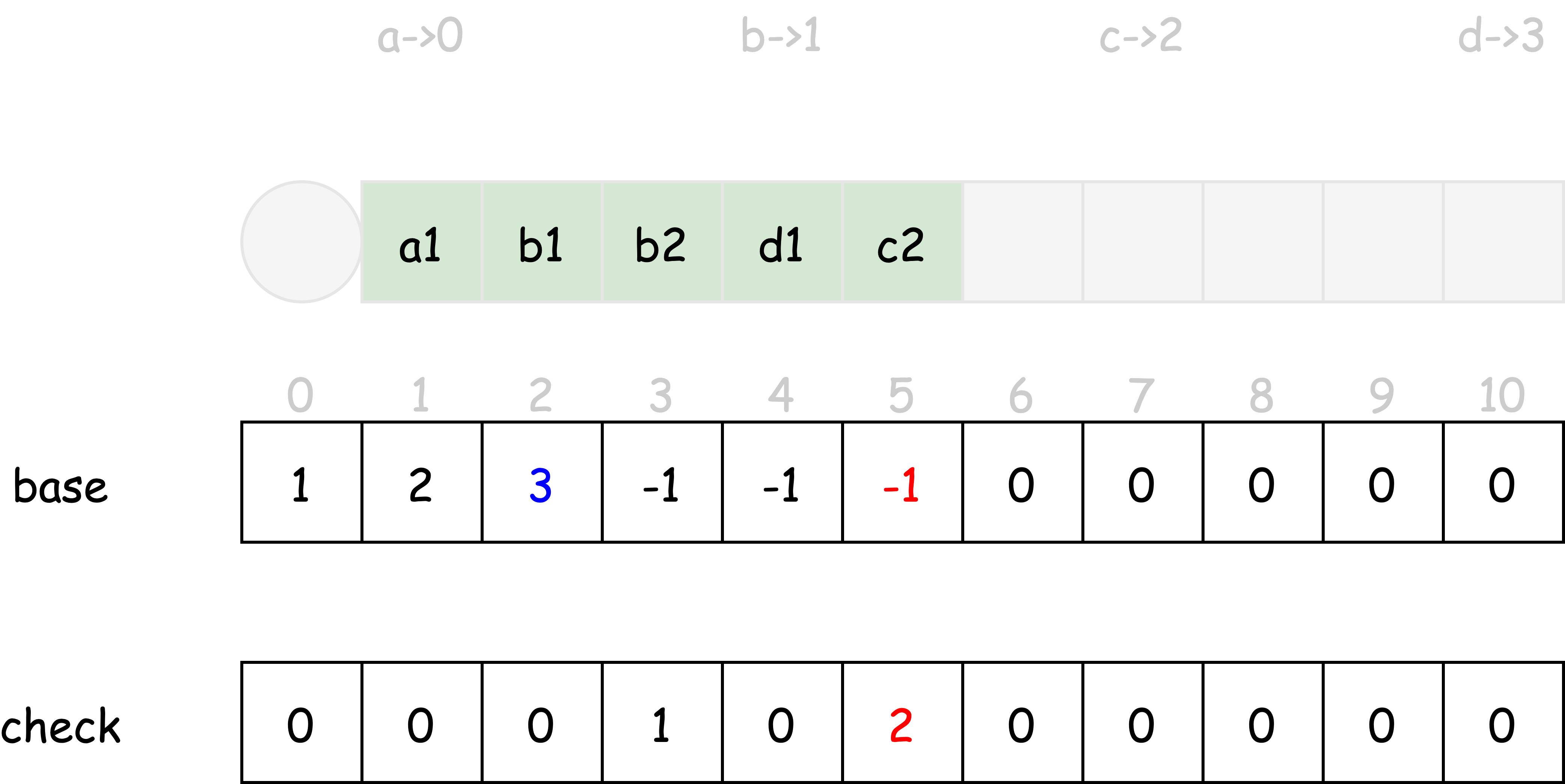
状态 b1 可以基于输入字符 c 转移到状态 c2，有

• $c2 = base[b1] + index(c) = base[b1] + 2$

由于下标为 3, 4 的数组元素都被占用，选择 $base[b1] = 3$ 则 $c2 = 5$，分别将 $base[5]$, $check[5]$ 改写。

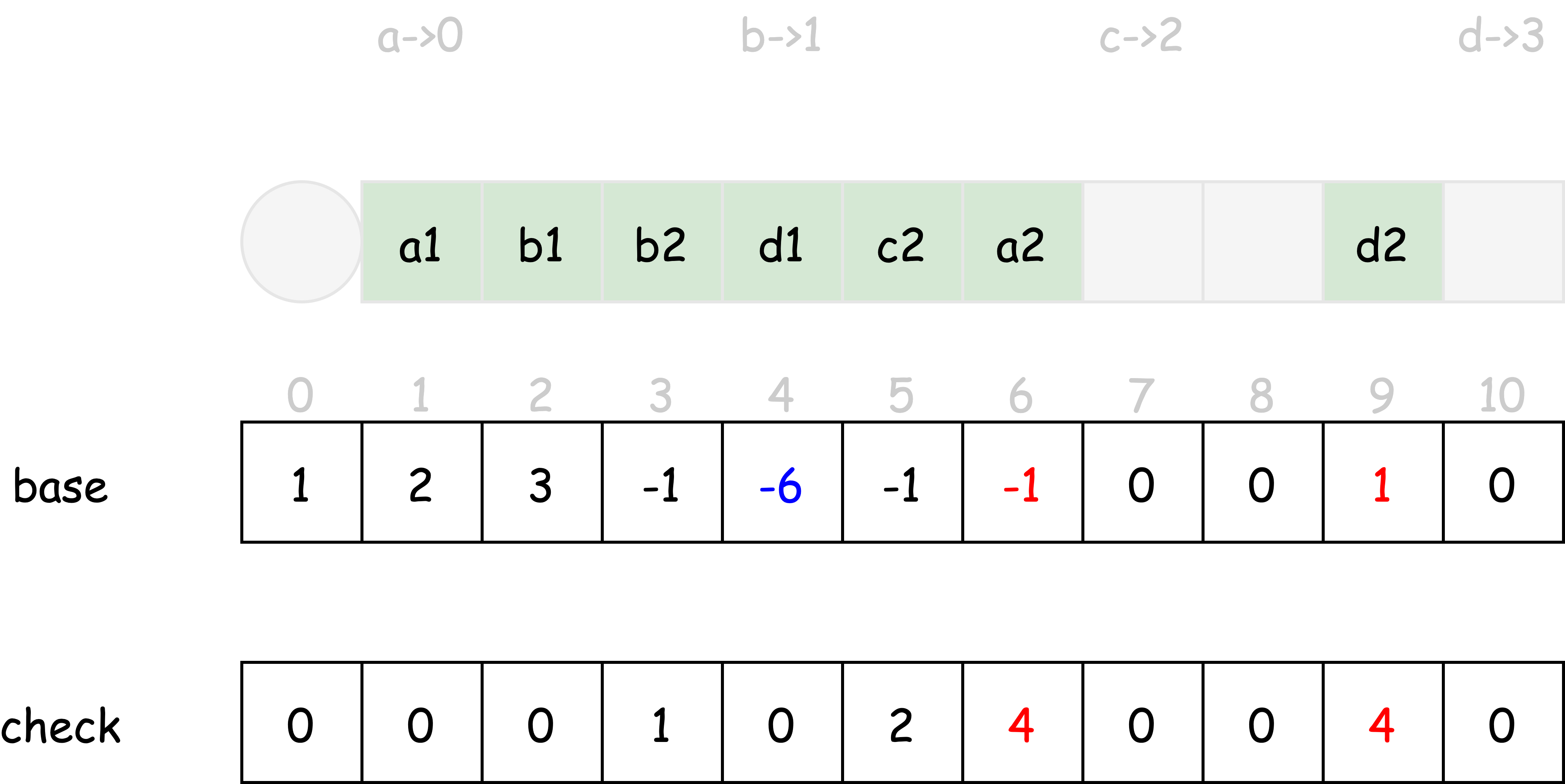
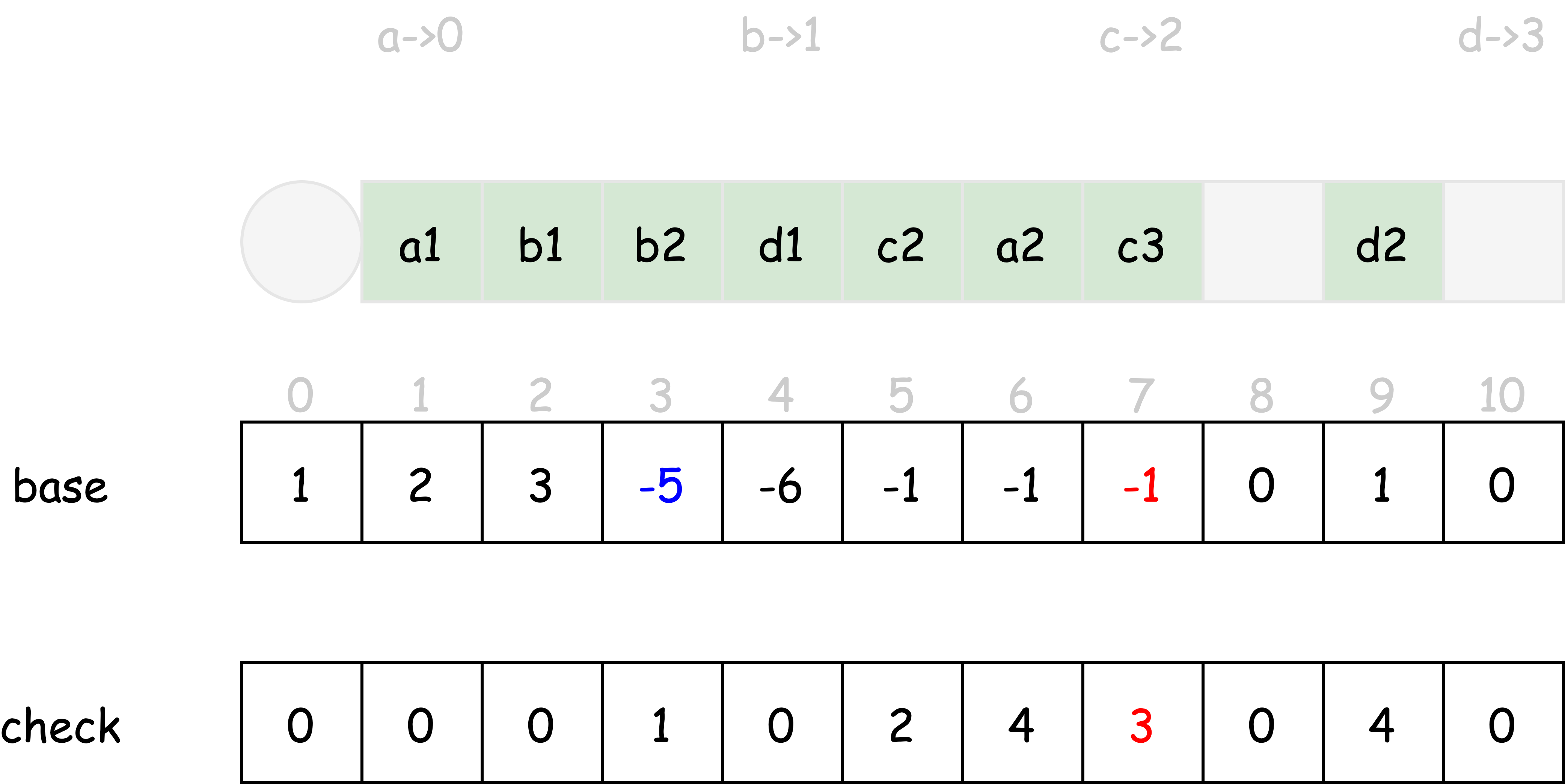
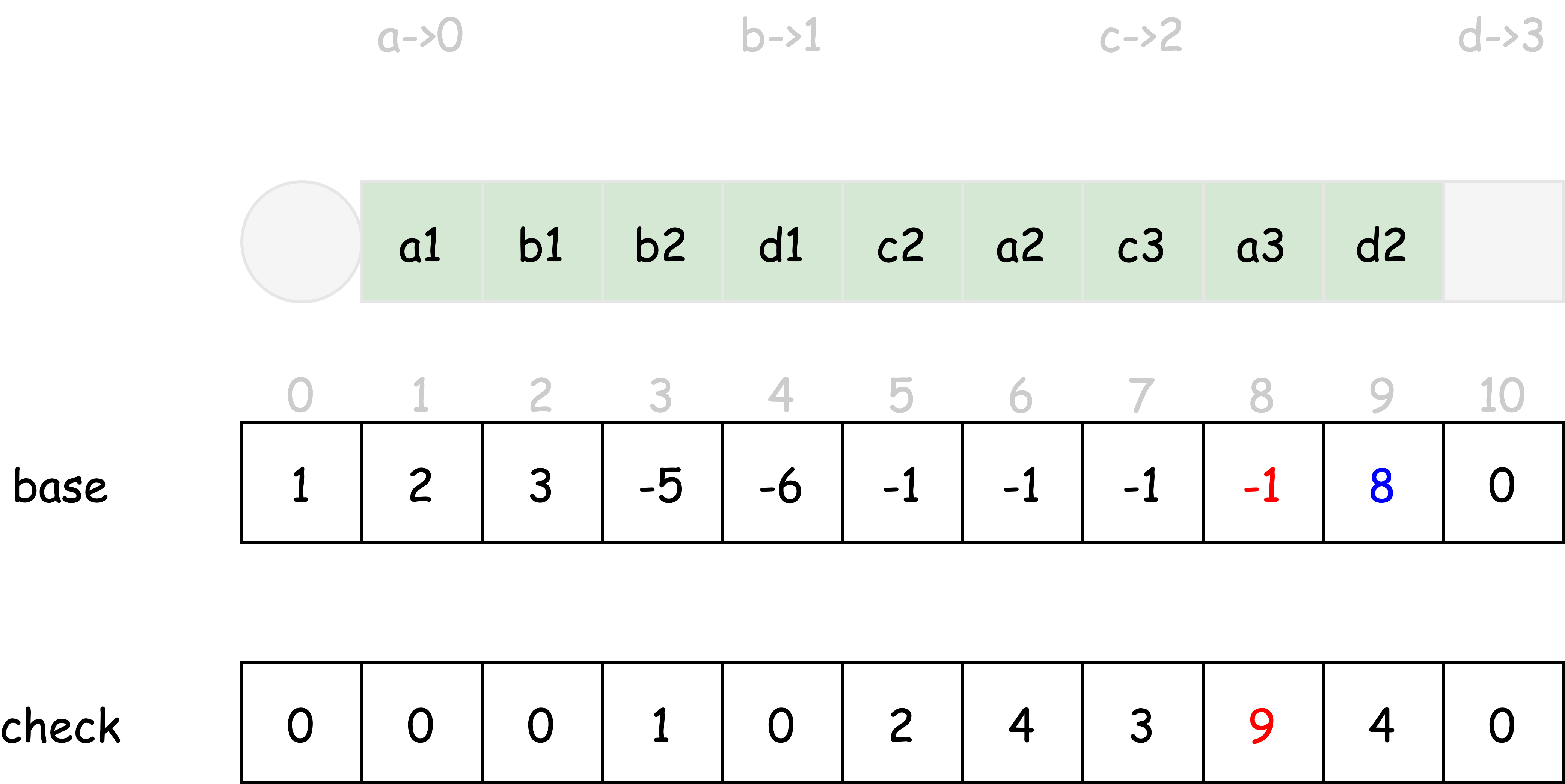
以此类推，直到所有的状态转移均通过 base, check 数组描述为止。

六、小结

双数组前缀树降低空间复杂度不是没有代价的，虽然查询效率不受影响，但构建复杂，而且添加词语的操作也具有相当高的时间复杂度。

一般来说，构建动作完成之后，为了在词库不变的情况下能够快速重建前缀树，会采取 Dump 的方式存储 base, check 数组以便下次直接读取。

总而言之，双数组前缀树适合高速查询低频更新词库的场景。对于 CJK 词库，能够极大地降低整个树的空间占用。